Deep Learning 기초1 (ML 기초)

January 25, 2019

김성훈 교수님의 “모두를 위한 머신러닝/딥러닝 강의(시즌1)”를 듣고 내용을 정리해 둔다. 참고한 문서들은 가장 아래 적어 둔다.

이제부터 야자체로 적을거야. 내가 강의를 들으면서 생각한 것들 말이야. 전공도 아니고 공부도 짧아. 틀리는 내용도 좀 있을거야. 주의해 주기 바래.

Introduction

보통 어떤 분야를 시작하기 전에 그 분야가 뭘 하는 것인지, 무엇을 위한 것인지, 누가 어떻게 만들었고 발전해 왔는지를 알면 큰 줄기를 알 수 있어.

What is Machine learning

Field of study that gives computers the ability to learn without being explicitly programmed _ Arthur Samuel (1959)

Machine Learning（ML）은 뭘 하는 것일까. 이 개념을 처음 만든 사람은 Arthur Samuel이라는 사람이야. 없던 개념을 만들거나 모호한 개념을 확정한다는 것은 대단한 식견이 있어야 가능한거야. 그래서 나는 이런 사람들은 개념을 만든 것 자체만으로도 대단한 업적을 남긴 것이라고 생각해.

처음 시작은 이런 거야. 컴퓨터에게 일을 시키고 싶은데, 이녀석이 단순해서 일일이 하나하나 설명해 줘야만 하는거야. 하지만 내가 편하려고 쓰는 건데 일일이 설명해 주려니 귀찮지. 니가 좀 알아서 해주면 얼마나 좋겠어. 그래서 생각해 낸 것이 ML이야. 내가 데이터만 넣어줄께. 그러면 너 혼자 익혀서 일 좀 하라는 거지.

In general, a learning problem considers a set of n samples of data and then tries to predict properties of unknown data _ An introduction to machine learning with scikit-learn

현실 세계에서 ML은 무엇을 위해 사용될까. 잘 몰랐던 사실을 발견하거나 새로운 인사이트를 얻는 등의 목적도 있지만, 가장 중요한 목적은 바로 예측이야. 새로운 값이 주어졌을 때 적당한 답을 말해주고, 과거와 현재를 바탕으로 미래에 대해 이야기해 달라는거지. 우리가 ML이라는 분야를 공부하는 것은 바로 예측을 하기 위해서야.

예측을 하면 뭐가 좋은데? 예측할 수 있게 되면 두려워하지 않아도 되고 통제할 수 있게 되지. 사실 인류가 철학을, 종교를, 과학을 발전시켰던 이유도 따지고 보면 이해하고 예측해서 마지막에는 통제하고 싶어서야. 따지고 보면 ML도 통제라는 인간의 근본적인 욕구의 발현 가운데 하나인 셈이지.

자, ML은 예측을 위한 거야. 그러기 위해 기계 스스로 학습했으면 좋겠어. 그게 ML이야. 그런데 그냥 ‘학습해’ 하고 말하고 끝내면 좋겠지만, 아무리 생각해도 학습할 데이터 정도는 주고 시켜야 할 것 같아. 그리고 어떤 식으로 배우라는 것도 이야기 해 주어야겠지. 그래서 ‘학습할 데이터’와 ‘학습 방법’이 관건이 되는 거야.

What is learning

▶ Supervised Learning : learninig with labeled examples ( training set )

Regression
binary Classification
multi-label Classification

▶ Unsupervised Learning : learning with un-labeled data

clustering
density estimation
dimension reduction

ML은 데이터와 학습할 문제에 따라 이렇게 구분을 해. 하지만 고급기술들은 대부분 Supervised Learning에 대한 것이야. 정답이 있는 데이터를 가지고 학습 시키기 때문에 예측이라는 목적에 더 적합하지. 방법들에 대한 평가나 비교도 가능하고 말이야. 그래서 여기에서는 주로 Supervised Learning에에 대해 이야기 할 거야.

반면 Unsupervised Learning은 답안이 없는 연습 문제와 같아서 풀어도 맞는지 틀리는지 알 수가 없어. 그래서 평가를 못해. 난처하지. 그래서 예측 보다는 데이터를 관찰하는데 더 많이 쓰이는 것 같아.

Data

데이터 측면에서 따져보자. 우선 학습을 위해 정답이 있는 학습 데이터가 필요해. training set이라고 해. 일종의 연습문제 같은거야. 그리고 본래 궁금한 물음이 있겠지. test set이라고 해. 본시험 같은 거지. 하지만 연구에서는 학습 성능을 따져보기 위해 test set도 정답을 가지고 있는 경우가 많아.

학습은 어떤 조건에 대한 답을 찾아내는 거야. 조건은 주어지는 거고 답은 찾아낼 대상이지. 함수에서 독립변수 종속변수 하는 거랑 같은거야. 그래서 전자를 x, 후자를 y라고 해. 때때로 후자를 target이라거나 label이라고 하기도 해.

학습에 대한 평가는 학습으로 도출된 예측값과 실제 관찰값의 차이로 할 수 있지. 학습은 이 차이를 줄이는 방향으로 계속 진행되어야 해. 그러므로 ML에는 ‘x를 보고 y를 예측해서 예측값 $\bar{Y}$를 출력하는 함수’와 ‘y와 $\bar{Y}$가 얼마나 차이가 있는지 따지는 함수’가 필요하지.

Data Set	입력값	관찰값	출력값（예측값）
Training Set	$X$	$Y$	$\bar{Y}$
Test Set	$X$	$Y$	$\bar{Y}$

우리가 만나는 데이터는 대부분 수치형 데이터나 범주형 데이터야. 그러니까 수치를 예측하는 문제가 있을 수 있고, 범주를 예측하는 문제가 있을 수 있어. 전자가 Regression이고 후자가 Classification이야.

How Do Machines Learn

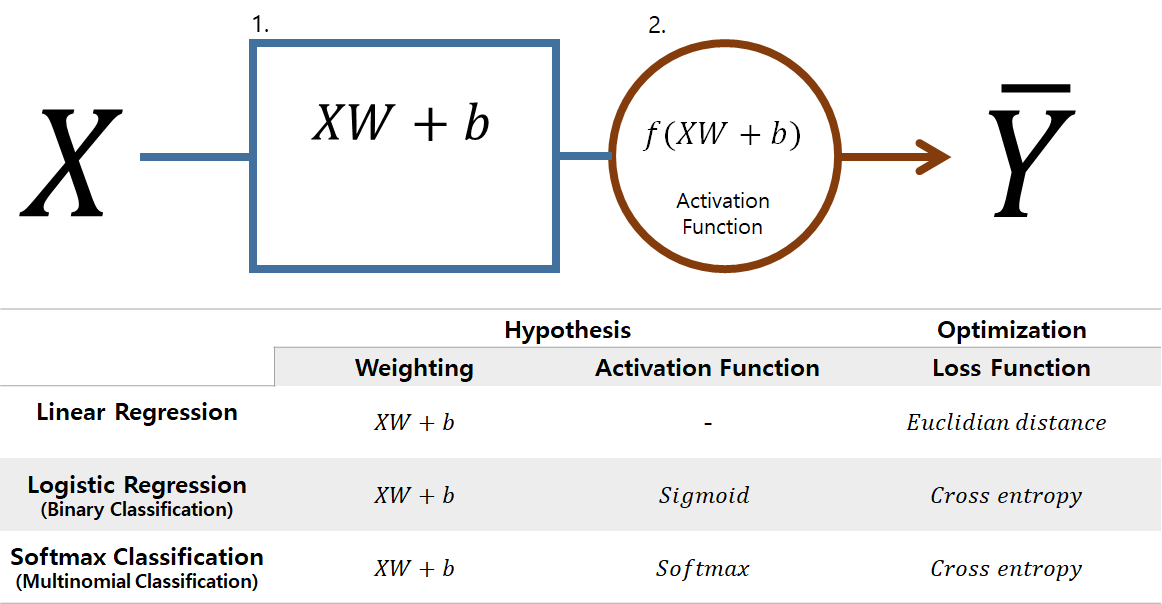
자, 이제 학습 방법에 대해 살펴볼꺼야. 먼저 큰 그림을 보자.

학습을 할 때는 크게 학습 대상에 대한 와꾸가 짜여져 있어야 해. 농구를 배우는 거랑 피아노를 배우는 거랑은 다르지. 수학을 공부하는 거랑 영어를 공부하는 것도 달라. 하지만 영어를 잘 배워 놓으면 독일어를 더 편하게 배울 수 있어. 이처럼 배움에는 어떤 틀이 필요하지. 이걸 Model이라고 해. 예를 들어 1, 2, 3 다음에 뭐지? 했을 때 4라고 한다면 이건 선형 모델로 와꾸를 짜고 있어서 그런거야. 현실 세계에 수치형 데이터들은 선형모델에 적합한 경우가 많아. 그래서 ML에서 선형모델을 기본으로 하고 있지. 이게 데이터가 이런 와꾸를 가지고 있다는 가정이기도 하기 때문에 아래에서는 Hypothesis라고 할꺼야. （위에서 ‘x를 보고 y를 예측해서 예측값 $\bar{Y}$를 출력하는 함수’라고 했던 것）

다음으로 중요한 것은 일단 해보고, 정답과 맞춰보고, 차이를 줄여 다시 해 보고, 다시 정답과 맞춰보고 … 이런 과정을 반복해야해. 기계도 비슷해. 그럼 정답과의 차이를 정량화 할 수 있어야해. 그리고 이것을 모니터링 하면서 줄여나가는 방향으로 학습을 진행해야 하지. 이 차이를 함수로 구현한 것을 Loss Function 또는 Cost Function이라고 해. 학습의 목적이 된다고 해서 목적함수(Objective Function)라고도 하지. （위에서 ‘y와 $\bar{Y}$가 얼마나 차이가 있는지 따지는 함수’라고 했던 것）

정리하면 이런거야. 먼저 데이터가 어떤 식으로 변해 갈거라는 가정（Hypothesis）이 필요해. 그 가정을 통해 수식을 만들어 값을 예측해 낼거야. 그러면 처음의 수식을 개선하기 위해 예측해 낸 값（$\bar{y}$）과 실제값（$y$）의 차이를 측정해야 해（Loss Function）. 그러면 우리는 이 차이를 좁혀나가는 방식으로 예측하는 수식을 개선해 나가는거야. 수식을 개선한다는 것은 정해진 와꾸가 있기 때문에 사실상 상수값을 조정하는 거야.

주어진 데이터와 예측 목적에 따라 이 Hypothesis와 Cost Function이 조금씩 달라져. 이걸 중심으로 방법들을 살펴보자.

Linear Regression

LR（Linear Regression）은 수치형 자료들을 학습해서 수치형 자료를 예측하기 위해 만들어졌어. 예를 들어 키를 주면 신발의 사이즈를 예측해 주는 문제와 같은 것이지. 키가 클 수록 신발 사이즈가 커지는 경향을 갖지. 우리가 접하는 많은 데이터들이 같이 커지거나 같이 작아지는 경향을 보이는 경우가 많아. 이걸 선형성(Linearity)이라고 하지. 그래서 이름이 Linear Regression이야.

▶ DATA

Training Set
- X : 수치형 자료
- Y : 수치형 자료
Test set
- X : 수치형 자료
- Y : 예측 목표

가정은 선형성을 표현해야 하므로 1차 함수로 표현할 수 있어. 관건이 되는 것은 Weight（W）과 bias（b）이지. 이 두 숫자를 적절하게 정하는 것이 학습의 관건이 되는 거야.

▶ Hypothesis (Linear)

주어진 데이터는 1차 함수（linear）로 표현될 수 있다.

\[H_L(x) = \bar{Y} = Wx + b\]

“적절하게 정한다”는 것을 어려운 말로 “최적화”라고해. 최적화를 하기 위해서는 우리가 알고 싶은 것과의 차이를 정량화할 수 있어야 해. 최적화의 목적이 된다는 면에서 목적함수（Objective Function）라고 하고, 알고 싶은 것과의 차이를 나타낸다는 면에서 Cost Function 혹은 Loss Function이라고도 해.

LR의 목적함수는 예측값과 실제값의 차이를 보는데, 분산（Variance）을 계산할 때처럼 거리의 제곱을 해서 평균을 내주는 방법을 사용해. 제곱을 하는 이유는 음수를 없애고 양수로 만들어주는 효과도 있고, 거리의 차이가 클 수록 패널티를 주는 효과도 있지.

▶ Objective Function

Cost Function (loss function)이 된다.
추정값과 실제값 사이의 차이（각각을 제곱해 평균）이다.

\[cost(W,b) = {1 \over m} \sum_{i=1}^m { (\bar{Y} - y_i)^2 }\]

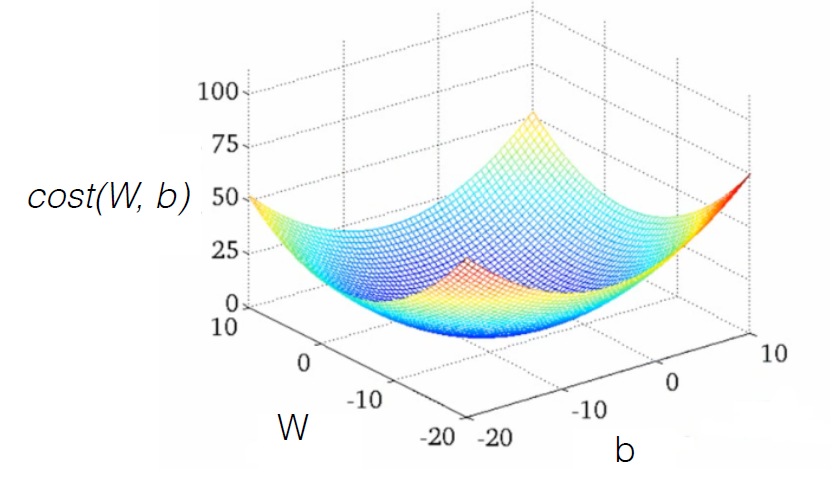
마지막 단계는 목적함수를 최적화 해서 W와 b를 찾아가는 방법이야. 이 부분이 바로 학습에 해당하는 거지. 직관적으로 가장 비용이 낮은 곳을 찾으면 되는데, 목적함수가 움푹한 형태의 함수일 때는 변화가 거의 없는 상태를 의미하게 되지. 이걸 수식으로 표현하면 목적함수를 미분해서 변화가 적어지는 방향으로 W와 b의 값을 조정해 나가면 된다는 거야.

걱정하지마. 이 작업은 컴퓨터에게 시킬꺼야. 앞에서 말했듯이 우리가 해야 할 일은 학습 데이터와 학습 방법을 정해지는 일 뿐이야.

▶ Optimization Goal

$cost(W,b)$를 최소로 하는 W, b를 구하는 문제!
$cost(W,b)$ 함수는 아래로 볼록한（Convex） W에 대한 2차 함수이므로
W를 갱신하면서 기울기가 작아지는 쪽（미분 사용）으로 W를 찾아나간다.
이것이 Gradiant descent algorithm이다.
여기서 $\alpha$가 learning rate이 된다. 보통 0.01로 시작한다.

\[\begin{matrix} W := W - \alpha { \partial \over \partial W } cost(W)\\ W := W - \alpha {1 \over m} \sum_{i=1}^m { ( Wx_i - y_i ) x_i } \end{matrix}\]

이 부분을 python 코드로 구현한 것을 보자. ☞ DeepLearningZeroToAll/lab-02-1-linear_regression.py

Linear Regression (일반화)

위의 문제는 x가 하나인 경우야. 하지만 현실에서는 여러개의 변수를 주고 예측하는 문제가 많지. 따라서 이 문제를 Multi variable의 문제로 일반화 시킬 수 있어.

수식에서 달라진 점은 변수에 따라 Weight가 하나씩 더 생겨났다는 점이지.

▶ Hypothesis

\[H(x_1,x_2,...,x_n) = w_1x_1+w_1x_1+ ... +w_nx_n + b\]

▶ Objective Function

\[cost(W,b) = {1 \over m} \sum_{i=1}^m { (H(x_{1i}, x_{2i}, ...,x_{ni}) - y_i)^2 }\]

다항식은 Matrix로 표현할 수 있어. 그러므로 변수가 A,B,C 3가지라면 아래처럼 표현할 수 있지.

\[\begin{pmatrix} x_{1A} & x_{1B} & x_{1C} \\ x_{2A} & x_{2B} & x_{2B} \\ ...\\ x_{nA} & x_{nB} & x_{nC} \\ \end{pmatrix} \bullet \begin{pmatrix} w_A \\ w_B \\ w_C \end{pmatrix} = \begin{pmatrix} x_{1A}w_{A} + x_{1B}w_{B} + x_{1C}w_{C} \\ x_{2A}w_{A} + x_{2B}w_{B} + x_{2C}w_{C} \\ ...\\ x_{nA}w_{A} + x_{nB}w_{B} + x_{nC}w_{C} \\ \end{pmatrix} = \begin{pmatrix} \bar{y}_{1} \\ \bar{y}_{2} \\ ...\\ \bar{y}_{n} \\ \end{pmatrix}\]

training set
- 입력값（x）의 Shape : X[n, 3] （데이터 개수는 $n$개, 변수는 $3$개 ）
- 출력값（y）의 Shape : Y[n, 1]
Weight의 Shape : W[3,1]
- 3은 입력값의 column 개수, 1은 출력값의 column 개수라고 할 수 있다.
- 3차원 vector를 1차원으로 축소하는 선형 변환을 의미한다.
- ∴ Weight의 차원을 보면, x와 y의 shape을 알 수 있다.

그러므로 위의 식은 Matrix를 이용하여 아래와 같이 쓸 수 있어.

▶ Hypothesis

\[H_L(X)= \bar{Y} = XW\]

▶ Objective Function

\[cost(W) = {1 \over m} \sum (\bar{Y}-y)^2 = {1 \over m} \sum (XW-y)^2\]

▶ Gradient desent

\[W := W - \alpha { \partial \over \partial W } cost(W)\]

Logistic Regression (Binary Classification)

때때로 수치형 데이터가 있을 때 범주형 데이터를 예측하고 싶을 때가 있어. 예를 들어 학생들의 점수에 따라 합격과 불합격을 나누는 문제야. 이런 문제를 위해 고안된 것이 LR（Logistic Regression）이야.

▶ DATA

Training Set
- X : 수치형 자료
- Y : 범주형 자료 ( binary의 경우 0 or 1)
Test set
- X : 수치형 자료
- Y : 예측 목표

합격과 불합격은 선형 모델로는 표현할 수가 없어. 그래서 값이 0에서 1 사이를 나타내는 특별한 함수를 적용하게 되었는데, 이를 sigmoid라고 해. 더 정확히 말하면, 선형 모델의 결과를 다시 sigmoid 함수에 넣어주는 거야. 코드로 나타내면 이런 거랄까. 그래서 형태는 바뀌었지만 여전히 W와 b를 정하는 문제로 귀결되게 되지.

sigmoid( linear_model( x ) )

▶ Hypothesis

주어진 데이터는 0에서 1 사이의 값을 갖는 sigmod 형태（graph@desmos.com）로 표현될 수 있다.
여기서 $g(Z)$는 activation function에 해당한다.

\[H_L(x) = Z = XW + b\] \[g(Z) = { 1 \over 1 + e^{-z} }\] \[H_R(x) = g(Z) = g( H_L(x) )\] \[∴ H_R(x) = \bar{Y} = { 1 \over { 1 + e^{-Z(x)} } } = { 1 \over { 1 + e^{-XW} } }\]

가정이 바뀌었기 때문에 Loss function도 그대로 사용할 수 없게 되었어. 선형모델은 공간에서의 거리를 측정하면 됐지만, 여기에서는 O, X를 맞추는 문제이기 때문에 거리가 의미를 가지지 않아. 그래서 cross-entropy라를 방법을 사용하게 되지.

▶ Objective Function

graph가 convex한 형태가 되는 function을 찾아야 한다.
거리에 제곱을 하는 대신 거리에 log를 취한다. （본래의 식이 지수함수이므로） graph@desmos.com

\[cost( \bar{y},y ) = \begin{cases} -log( \bar{y}-0 ) : y = 0\\ -log( 1-\bar{y} ) : y = 1 \end{cases}\] \[cost( \bar{y},y ) = - y\log( \bar{y} ) - (1-y)\log(1-\bar{y})\] \[∴ cost( W ) = -{1 \over m } \sum { y\log( H(x) ) + (1-y)\log(1-H(x)) }\]

▶ Optimization Goal

$cost(W,b)$를 최소로 하는 W, b를 구하는 문제!
cost function이 convex한 형태이므로, 역시 Gradiant descent algorithm으로 해결할 수 있다.

Softmax Classification (Multinomial Classification)

LR은 O, X의 문제에만 사용할 수 있어. 그럼 K가지로 class를 나누어야 한다면 어떻게 해야 할까.

▶ DATA

Training Set
- X : 수치형 자료
- Y : 범주형 자료 ( Multinomial의 경우 k개의 범주)
Test set
- X : 수치형 자료
- Y : 예측 목표

직관적으로 생각해 보면, LR을 여러다발 묶어서 판별식을 만들면 해결될 수 있을 거야. 위에서 본 다항식의 예처럼 각각의 W와 b가 주어져야 할꺼야. 그리고 일일이 sigmoid를 넣어 주면 복잡하니까 sigmoid처럼 특별한 함수를 생각해 냈어. 그것이 softmax 함수야.

▶ Hypothesis

Logistic Classifier를 여러다발로 묶어 사용하는 문제로 볼 수 있다.
각각의 Logistic Classifier에 대한 Weight이 따로 생성되어야 한다. class의 개수 만큼의 column vector를 가지는 matrix W가 필요하다.
train data set의 개수가 n, class의 종류가 A, B, C 등 K까지라면, 각각의 column vector（$[w_{1J}, w_{2J}, w_{3J}]$）들은 Logistic Classifier에 해당한다.

\[XW = \bar{Y}\] \[\begin{pmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ ...\\ x_{n1} & x_{n2} & x_{n3} \\ \end{pmatrix} \bullet \begin{pmatrix} w_{1A} & w_{1B} & ... & w_{1K} \\ w_{2A} & w_{2B} & ... & w_{2K} \\ w_{3A} & w_{3B} & ... & w_{3K} \\ \end{pmatrix} =\begin{pmatrix} \bar{y}_{1A} & \bar{y}_{1B} & ... & \bar{y}_{1K} \\ \bar{y}_{2A} & \bar{y}_{2B} & ... & \bar{y}_{2K} \\ ...\\ \bar{y}_{nA} & \bar{y}_{nB} & ... & \bar{y}_{nK} \\ \end{pmatrix}\]

예측값（$\bar{Y}$）의 row vector（[$\bar{y}{iA}, \bar{y}{iB}, …, \bar{y}_{iK}$]）는 i번째 클래스에 해당할 Score라고 볼 수 있다. 즉 가장 높은 값에 해당하는 클래스일 가능성이 가장 크겠다.
현재 score 값인 row vector의 값을 0에서 1사이의 확률 값으로 바꾸어 주기 위해 Softmax Function을 사용한다.
만약 $\bar{Y}$의 row vector가 [2.0, 1.0, 0.1]이라면, Softmax Fucntion을 통해 [0.7, 0.2, 0.1]의 확률값을 얻을 수 있다. （합계가 1이 된다） 이때 0.7이 가장 큰 값이 되므로 첫번째 class가 예측값이 된다.
여기서 Softmax Function은 activation function에 해당한다.

\[S(y_i) = { e^y_i \over \sum {e^y_i} }\]

▶ Objective Function

Cross-entropy cost function을 사용한다. graph@desmos.com

\[cost( H(x),y ) = D(\bar{Y}, Y) = - \sum_i^k { y_i \log( \bar{y} ) }\]

$\bar{Y}$ = [0.7, 0.2, 0.1]이고 $Y$ = [1.0, 0.0, 0.0]이라면 $cost$는 다음과 같이 된다.

\[cost = - ( 1 \times \log(0.7) + 0 \times \log(0.2) + 0 \times log(0.1) )\]

전체 데이터에 대해서 Cost Function은 다음과 같다.

\[\begin{matrix} cost( \bar{Y},y ) = {1 \over N} \sum_i { D(\bar{Y}, Y) }\\ cost( H(x),y ) = {1 \over N} \sum_i { D(H(x_i), y_i) }\\ \end{matrix}\] \[cost( H(x),y ) = {1 \over N} \sum_i { D( S(wx_i + b), y_i) }\\\]

▶ Optimization Goal